In A Christmas for Shacktown pubblicato la prima volta nel gennaio del 1952 (in italiano ‘Zio Paperone e il ventino fatale’), uno dei più bei lavori di Carl Barks, Zio Paperone rischia di perdere tutto il denaro contenuto nel suo deposito per il crollo del pavimento dell’edificio medesimo dovuto al carico di monete e banconote in esso stipate. La causa che scatena il disastro è una misera monetina: il ‘ventino fatale’ (o ‘decino’, secondo altre versioni) del titolo. Questo esempio è solo uno dei tanti che sono usualmente associati al termine di ‘catastrofe’ intesa come l’emergere improvviso di un effetto dirompente in conseguenza di una causa che può essere di lieve entità o che comunque esercita la sua influenza con continuità nel tempo, senza apparenti effetti fino al momento del crac. Per rimanere nella storia di Carl Barks, per anni ed anni monete sono state aggiunte una dopo l’altra nel deposito, in un processo di accumulo di tipo continuo e senza alcuna sofferenza degna di nota per la struttura dell’edificio. Ad un certo momento, improvvisamente, appare una discontinuità ed il crac (o rumble nella vignetta) ne è l’esito inaspettato.

La nascita della ‘teoria delle catastrofi’, come teoria matematica, si fa usualmente risalire al 1972 con la pubblicazione del libro Stabilité Structurelle et Morphogénèse. Essai d’une théorie générale des modèles del matematico francese René Thom (1923-2002). Il libro, soprattutto dopo la sua traduzione in lingua inglese, ebbe un grandissimo impatto anche se forse ancora oggi, dato il suo stile complesso, non è stato ben compreso da molti.

Entrato nel 1943 alla prestigiosa École Normale Supérieure di Parigi e laureatosi nel 1946, René Thom ottenne una posizione di ricerca del CNRS a Strasburgo. Dopo una borsa di studio che gli permise di passare un periodo negli Stati Uniti (dove incontrò anche Einstein) ebbe posizioni di insegnamento a Grenoble (1953-1954) e poi nuovamente a Strasburgo (1954-1963). Fu nominato professore nel 1957. Nel 1958, a 35 anni, gli fu assegnata la ‘medaglia Fields’ per i suoi importanti contributi in topologia differenziale e nella teoria delle singolarità, alcuni dei quali risalenti già al lavoro di ricerca con cui concluse il suo dottorato nel 1951. In occasione del discorso di presentazione per il conferimento della medaglia Fields si mise in particolare evidenza come le idee di Thom, degne di ammirazione per la loro potenza geometrica e la loro natura intuitiva, avessero arricchito la matematica e come tutto sembrasse indicare che l’impatto di tali idee (sia quelle già espresse nei lavori pubblicati, sia quelle dei lavori a venire) fosse lungi dall’essere esaurito. Nel 1964 René Thom si trasferì all’‘Institut des Hautes Études Scientifiques’ di Bures-sur-Yvette, un centro di ricerca vicino a Parigi, dove continuò a lavorare fino al pensionamento, nel 1988.

Anche se la teoria delle catastrofi ha le sue radici nelle ricerche di topologia differenziale per cui Thom fu insignito della medaglia Fields, il suo sviluppo è negli anni successivi al 1960. Thom stesso in alcuni articoli autobiografici afferma che la medaglia Fields gli garantì la libertà di scegliere le ricerche che più desiderava sviluppare, senza alcun vincolo. Questo lo portò ad abbandonare gradualmente le ricerche matematiche in senso puramente tecnico del termine e ad abbracciare nozioni più generali, quali la genesi delle forme in biologia, in geologia, nella linguistica, nelle scienze sociali ed in altri campi ancora, e affidandosi sempre di più alla sua intuizione geometrica piuttosto che al formalismo matematico di tipo accademico.

Non si può concludere questa breve nota storica senza menzionare il nome di Erik Christopher Zeeman (nato nel 1925), matematico inglese che contribuì alla diffusione della teoria e delle sue applicazioni con una serie di appassionanti articoli e conferenze. Chris Zeeman è una figura importante nel panorama della matematica britannica del Novecento. Laureato a Cambridge, nel 1964 si trasferì nella nuova Università di Warwick, a Coventry, dove rimase fino al 1988. Sotto la sua leadership, Warwick diventò in pochi anni uno dei centri di ricerca più importanti per lo studio dei sistemi dinamici. Oltre che per i suoi notevoli successi nella ricerca matematica e nel mondo accademico che gli hanno garantito un numero molto ampio di onorificenze (fino al titolo di ‘Sir’), Christopher Zeeman è famoso per le sue brillanti lezioni e conferenze e per la sua lungimirante opera in favore dell’educazione dei giovani talenti matematici nel Regno Unito. Se la teoria delle catastrofi divenne così popolare al di fuori del mondo matematico, tanto che persino i quotidiani cominciarono ad occuparsene alla metà degli anni Settanta con titoli come «Thom: ho la formula che spiega i disastri» («Corriere della Sera Illustrato», 1978), lo si deve in gran parte anche all’opera entusiastica di conferenze ed articoli di Zeeman, un vero pioniere per quanto riguarda l’immaginare nuove applicazioni della teoria alle scienze biologiche e comportamentali e ideatore di una ‘macchina delle catastrofi’, un semplice meccanismo che illustra come piccole perturbazioni possano dare luogo a fenomeni di discontinuità. Secondo lo stesso Thom, il termine ‘teoria delle catastrofi’ sarebbe stato coniato proprio da Zeeman.

Il grande successo di pubblico ottenuto dalla teoria delle catastrofi negli anni Settanta portò ad una ‘moda’ per cui sempre più persone, imitando l’approccio di Thom e Zeeman (e a volte senza nemmeno comprendere a fondo le tecniche che stavano utilizzando e non possedendo la padronanza matematica o l’intuizione geometrica di questi due precursori), tentarono di trovare nuove applicazioni della teoria a speculazioni via via più ardite o stravaganti e, alle volte, prive di ogni fondamento sperimentale. Ciò provocò una sorta di rigetto da parte di una grossa fetta della comunità matematica (e scientifica in generale) a cui seguì un periodo di accesi dibattiti e polemiche. Lo stesso René Thom, in un suo articolo autobiografico, nel 1997, concludeva amaramente che «è un fatto che la teoria delle catastrofi sia morta. Ma si potrebbe dire che è morta a causa del suo grande successo… Quando ci si rese conto che la teoria non permetteva previsioni quantitative, tutte le menti benpensanti decisero che era priva di valore…». Oggi si può vedere il tutto da una prospettiva storica e, invece di scrivere come in un famoso articolo del 1977 su «Science» (Gina Kolata): «Teoria delle catastrofi: il re è nudo», si può pubblicare lavori dal titolo «Ascesa e caduta della teoria delle catastrofi in economia: si è gettato via il bambino assieme all’acqua sporca?» (J.B. Rosser Jr., 2007). Torneremo su questo punto più avanti.

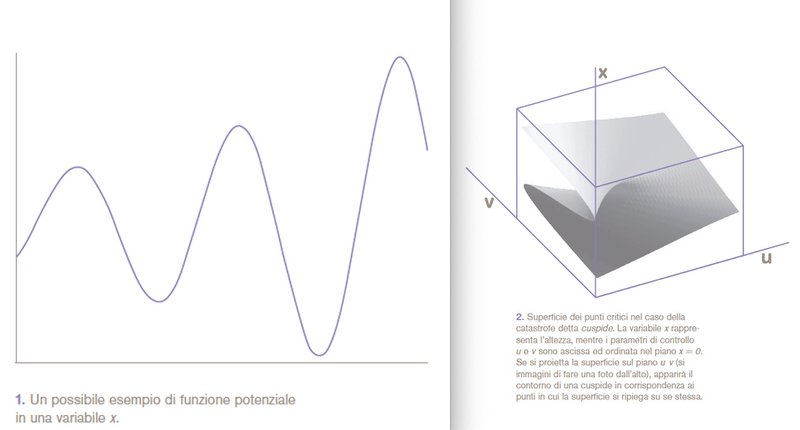
La teoria delle catastrofi si propone di dare una spiegazione di alcuni fenomeni di tipo discontinuo mediante l’utilizzo di modelli matematici di tipo continuo. Un sistema (un sistema fisico o meccanico, un organismo vivente, un modello economico o sociale, ecc.) viene modellato mediante equazioni differenziali. Queste rappresentano l’evoluzione del sistema nel tempo. Per chi legge, non è necessario sapere in dettaglio (o ricordarsi, se l’ha dimenticato) che cosa sia un’equazione differenziale; per ora è sufficiente sapere che c’è una dinamica interna al sistema per cui l’evoluzione di questo è descritta in modo simile alle leggi della fisica. Una prima importante ipotesi di lavoro che viene assunta è che il sistema sia di tipo gradiente, nel senso che c’è una funzione potenziale dalla conoscenza della quale è possibile dedurre gli stati stazionari in cui il sistema si troverà in equilibrio. Una funzione potenziale V è una funzione di un certo numero di variabili x, y, z… (variabili interne che descrivono lo stato del sistema) e che assume come valori dei numeri reali. Un esempio classico in fisica è dato dall’energia del sistema che si sta considerando, ma si possono immaginare innumerevoli altri esempi in altre situazioni. Per semplicità di esposizione, immaginiamo per un momento che il potenziale dipenda da una sola variabile x. Avremo quindi una funzione V (x) di cui si può tracciare il grafico (figura 1).

Per un sistema di tipo gradiente il comportamento è analogo a quello di una goccia d’acqua (o di una pallina) appoggiata ad un punto del grafico e soggetta ad una forza che la spinga verso il basso. Essa tenderà a spostarsi nei punti di minimo relativo della funzione potenziale. Ci sono, a dire il vero, delle eccezioni. Per esempio se mettiamo la nostra goccia in un punto di massimo del potenziale (o in un punto di flesso in cui la derivata è nulla), la goccia potrebbe rimanere ferma ‘in bilico’. Tali posizioni sono però di tipo instabile, nel senso che basterà una minuscola perturbazione per far scivolare la nostra goccia verso un punto di minimo adiacente. Spesso i sistemi fisici (come pure altri sistemi in economia, in biologia, ecc.) si comportano in modo simile a quanto ora descritto, stabilizzandosi (dopo un certo tempo transitorio) verso le posizioni di equilibrio stabile date dai minimi relativi. Una seconda importante assunzione della teoria delle catastrofi è quella di trascurare il transitorio (che si suppone svolgersi in una scala dei tempi molto più piccola rispetto ai fenomeni che si vuole osservare) e di concentrarsi sulle posizioni di equilibrio stabili o instabili. Chiaramente, le prime sono quelle che si osservano in natura perché persistono per piccole variazioni delle condizioni iniziali. Nel caso semplice in esame, cioè di un potenziale V (x) dipendente da una sola variabile x, per individuare le posizioni di equilibrio basterà studiare l’equazione dei punti stazionari (o punti critici) V’(x) = 0 e trovarne le soluzioni.

Se tutta la storia si riducesse a questo, ci sarebbe ben poco da dire. Ciò non accade in natura, nel senso che la funzione potenziale V (x) in generale dipenderà da alcuni parametri (detti anche fattori di controllo) che potrebbero variare nel tempo. Per fare un esempio molto grossolano, la forma del nostro corpo è qualche cosa di stabile giorno per giorno (per fortuna!), ma non rimane la stessa nel corso degli anni. Si cresce, la pancia si gonfia, la schiena si curva un po’ e l’aitante e snello giovanotto di un tempo si trasforma con il passare degli anni in un meno aggraziato professore di mezza età. In quest’ottica, si può ipotizzare che la funzione potenziale V, oltre a dipendere da un certo numero di variabili interne x, y, z…, dipenda anche da un certo numero di parametri di controllo u, v, w… al variare dei quali varierà la forma della funzione V. Dato che (come abbiamo visto sopra) ci interessa individuare i punti stazionari di V, con particolare riguardo a quelli stabili, studieremo il modo in cui al variare dei parametri di controllo cambia la stabilità dei punti stazionari. Si può immaginare ora delle situazioni in cui al variare di certi parametri, un punto che prima era stabile perda la sua stabilità: la pallina (o gocciolina d’acqua) che tranquillamente giaceva a riposo in una conca, improvvisamente si troverà sul lato di un pendio e scivolerà via verso un nuovo punto di minimo del potenziale (o cadrà indefinitamente se tutti i punti di minimo sono svaniti). In tal caso, una variazione continua dei parametri viene a causare un salto discontinuo dello stato del sistema: una catastrofe, appunto! Le variazioni dei grafici di V al variare dei parametri di controllo si possono pensare come le variazioni di un territorio durante lo scorrere di ere geologiche. Se si potesse filmare un paesaggio, riprendendo un panorama apparentemente fisso ed immutabile (stabile) di colline e montagne per alcuni milioni di anni e si potesse poi rivedere il film ad altissima velocità, si osserverebbero colline ed avvallamenti del terreno nascere, modificarsi, sparire, ecc.

A questo punto entra in gioco la geometria, nel senso che lo stato in cui si trova il sistema verrà descritto dai punti di una superficie le cui coordinate sono costituite dai parametri di controllo e dalle variabili che descrivono lo stato del sistema nel caso stazionario. L’evoluzione del sistema al variare dei coefficienti di controllo verrà visto come un punto che si muove su tale superficie. Conoscere come sono fatte queste superfici permette di estrarre informazioni sulle possibili evoluzioni nel tempo dei sistemi che si stanno studiando. Le diverse superfici qualitativamente diverse vengono chiamate ‘catastrofi elementari’.

Si potrebbe credere che tutti i possibili casi qualitativamente diversi che uno possa concepire siano in numero enorme (se non infinito). Ciò renderebbe la teoria priva di utilizzo pratico, visto che chi volesse applicarla ad un modello specifico non saprebbe quale tipo di ‘catastrofe elementare’ scegliere. Qui sta uno dei punti cruciali, contenuto in un teorema di classificazione topologica di Thom (1969) secondo cui in senso generico e per sistemi dipendenti fino a tre parametri di controllo vi sono cinque catastrofi elementari. Per sistemi dipendenti fino ad un massimo di quattro parametri, ai cinque modelli precedenti di catastrofi se ne devono aggiungere altri due, per un totale di sette catastrofi elementari: il ‘magico numero 7’, così sacro per i teorici delle catastrofi, come scrive con una certa ironia Vladimir Arnol’d nell’introduzione del suo libro Teoria delle catastrofi (Torino 1990).

Le sette catastrofi elementari sono state battezzate con dei nomi suggestivi che ricordano alcune caratteristiche delle superfici descritte dagli insiemi dei punti critici della funzione potenziale.

L’esempio più semplice di catastrofe elementare viene detto piega. Entra in gioco in tutti quei modelli in cui un sistema procede in modo uniforme verso un punto di rottura, come nella storia della monetina che provoca il crollo del pavimento nel deposito di Zio Paperone. Tale situazione viene ben descritta da espressioni colloquiali come ‘la goccia che fa traboccare il vaso’ o ‘non tirare troppo la corda perché si rompe’. Dal punto di vista geometrico, la piega viene rappresentata come una superficie che si piega una sola volta nella forma di una parabola di equazione u = -x 2. Anticamente, alcuni credevano che la Terra non potesse essere rotonda perché chi fosse sceso verso l’equatore, proseguendo ancora sarebbe prima o poi caduto verso il basso. L’idea geometrica della catastrofe a piega è praticamente la stessa.

Oltre alla piega, i nomi attribuiti nella lingua italiana a tali sette catastrofi elementari sono i seguenti: la cuspide, nel caso di una variabile x e due parametri di controllo u, v, la coda di rondine, nel caso di una variabile x e tre parametri di controllo u, v, w, e ancora la farfalla, l’ombelico iperbolico (la vague), l’ombelico ellittico (le poil), l’ombelico parabolico (le champignon), per i quali non diamo l’espressione esplicita del potenziale per motivi di spazio.

La catastrofe a cuspide è quella che è stata forse maggiormente utilizzata in molteplici applicazioni, più o meno appropriate. Non è banale come la piega e quindi permette una descrizione di fenomeni più complessi. D’altra parte, l’insieme dei punti critici costituisce una superficie che si può visualizzare nello spazio (e non come nel caso delle catastrofi di ordine superiore che sono descritte geometricamente da superfici contenute in spazi di dimensione almeno 4 e delle quali sono pertanto visualizzabili solo alcune sezioni tridimensionali). Alexander Woodcock e Monte Davis in La teoria delle catastrofi (Milano 1982) utilizzano modelli basati la maggior parte delle volte sulla catastrofe a cuspide per descrivere non solo esempi ben noti della fisica, ma anche applicazioni più controverse (proposte da vari autori) quali il comportamento territoriale degli animali, l’aggressione o la sottomissione di un cane che venga provocato, alcune caratteristiche comportamentali come l’essere di temperamento solitario o gregario, comportamenti psicologici di massa relativi alla percezione del pericolo che possono aumentare o diminuire la coesione di un esercito, scatenare il panico, dare inizio a delle rivolte, ecc. Applicazioni alla politica e alla storia hanno tentato di descrivere il declino e la caduta dell’Impero Romano, l’ascesa di Hitler al potere in Germania o la ‘Primavera di Praga’ (quando uscì il libro non era ancora caduto il Muro di Berlino, altrimenti forse ci sarebbe stata anche una possibile applicazione ai fatti del 1989). La catastrofe a cuspide è stata utilizzata anche per spiegare eventi quali il battito cardiaco, i crolli in borsa, le rivolte carcerarie, le risse negli stadi di calcio ad opera di gruppi di tifosi facinorosi, l’alternarsi di periodi di censura a periodi di permissivismo relativamente alla diffusione della pornografia, le alterazioni del ritmo sonno-veglia e l’analisi di vari disturbi psichici.

Un esempio di tali applicazioni (attribuito alla fantasia di Zeeman), viene descritto da Arnol’d nel suo libro come segue: una personalità creativa (ad esempio uno scienziato) viene caratterizzato dai parametri x = relativo al successo, u = associato all’entusiasmo, v = relativo alla competenza tecnica. Con riferimento alla figura 2 (per avere una descrizione compatibile con il grafico, ipotizzo che valori piccoli di u corrispondano a un grande entusiasmo) immaginiamo di individuare la situazione in cui si trova ad un certo punto della sua esistenza la persona che viene analizzata. Se l’entusiasmo è piccolo (cioè u è grande), siamo lontani dalla zona della cuspide (nella parte destra della superficie). In questo caso non si verificherà nulla di inaspettato. Se la competenza tecnica v aumenta, aumenterà (lentamente) anche il successo, nel senso che il punto della superficie critica, che rappresenta la descrizione della personalità che viene analizzata, si sposterà da regioni più basse (in basso a destra) a regioni più alte (in alto a destra) della superficie. Se però l’entusiasmo è alto e quindi ci troviamo in una zona con u piccolo (nella zona più scura della superficie in basso a destra) al crescere di v (cioè aumentando la competenza) potremo entrare nella zona sotto alla piega. In tale caso, si ha un cambiamento improvviso nel senso che il punto (che rappresenta le tre caratteristiche associate alla persona) salta, nel momento in cui si incontra la cuspide, immediatamente sul punto che gli sta sopra nella parte alta della superficie. Poiché i punti con x basso da cui eravamo partiti corrispondono alla persona entusiasta ma con poca competenza tecnica e di poco successo (nel modello questa persona viene chiamata ‘maniaco’), l’esempio mostra come si possa balzare al successo (i punti con x alto sulla piega superiore della superficie rappresentano il successo di una persona entusiasta e competente, denominata ‘genio’ nell’esempio in questione). Naturalmente, ci può essere anche il percorso inverso: un entusiasta di successo non sorretto dalla corrispondente crescita di competenza potrà subitaneamente cadere nella parte inferiore della superficie finendo nella zona etichettata come ‘maniaco’.

Esempi di questo tipo sono altamente suggestivi ma offrono lo spazio a critiche anche feroci. A nessuno piace pensare che le manifestazioni della propria personalità siano descrivibili solamente con una grandezza e due parametri, al pari del modello del cane che, se provocato, può attaccare o cedere il passo. D’altra parte c’è da dire che soprattutto Thom e Zeeman avevano uno stile convincente e anche l’audacia intellettuale di proporre punti di vista nuovi basati su modelli di questo tipo. Arnol’d conclude più avanti nel suo libro affermando che «i bei risultati della teoria della singolarità non dipendono fortunatamente dal dark mysticism della teoria delle catastrofi».

E a proposito di misticismo, io invece desidero concludere con un aneddoto curioso: Salvador Dalì (1904-1989), il grande pittore surrealista, negli ultimi anni della sua vita (a partire dal 1978 circa) fu affascinato dalla teoria delle catastrofi. Conobbe personalmente René Thom e gli volle dedicare nel 1983 un quadro basato sul mito di Europa ed intitolato El rapto topólogico de Europa – Homenaje a René Thom. Il tema del dipinto è poi ripreso in un particolare del quadro La coda di rondine (‘La queue d’aronde – Série des catastrophes’) (figure 3-4). Il disegno centrale di quest’ultimo lavoro è direttamente tratto da una proiezione della figura quadridimensionale della catastrofe a coda di rondine di Thom. È noto che Dalì era affascinato dal concetto di quarta dimensione, che aveva esplorato in altri suoi dipinti precedenti. Nel quadro La coda di rondine sono presenti anche una cuspide ed un segno stilizzato musicale (associato alla figura di un violoncello) che però è anche il simbolo dell’integrale.

L’aneddotica racconta che Dalí riteneva che la sala di aspetto della stazione ferroviaria della città di Perpignan (Perpignano, capoluogo del dipartimento dei Pirenei orientali nella regione della Linguadoca-Rossiglione), dove aveva percepito (il 19 settembre del 1963) una visione di estasi cosmica, fosse il centro dell’universo. Vari anni dopo, egli ebbe il suo unico incontro con René Thom che gli confidò che in quel momento stava studiando la teoria della tettonica a placche e i movimenti della crosta terrestre. Ad una domanda del pittore catalano, sembra che il matematico francese confermasse che la penisola iberica aveva ruotato (alcuni milioni di anni prima) avendo come fulcro proprio il posto ove oggi si trova la stazione di Perpignan. L’artista dipinse successivamente il suo omaggio a René Thom riportando in basso a sinistra dell’opera esattamente l’espressione del potenziale che descrive la catastrofe a cuspide. Il quadro è uno degli ultimi dipinti di Dalí ed alcuni critici in un primo momento lo considerarono poco più di uno scarabocchio senile fatto da una persona che ormai soffriva di allucinazioni. Tuttavia, una critica successiva rivalutò l’opera, anzi si trovò un’incredibile somiglianza fra le fratture disegnate da Dalí sulla tela ed alcuni percorsi stradali verso Narbonne
(a nord di Perpignan)… Ma Dalí, a detta di testimoni, tracciò quei segni senza avere davanti a sé una mappa stradale della zona… Deliri di un vecchio folle o ultimi lampi di un genio?