Mi accingo a preparare questo breve articolo con il tentativo di trasmettere un pezzetto di matematica. Fare ricerca è il mio lavoro, ma è per me anche una sorta di rifugio, o di conforto. In una realtà piena di incertezza, la matematica fornisce infatti un campo di movimento della mente in cui le regole sono chiare e definite. La speranza sarebbe condividere un po’ di questo mondo. Ma come parlare di matematica? È una materia che non si lascia comunicare facilmente e gode della reputazione di essere inaccessibile. Quando dico che faccio matematica ricevo spesso una risposta al limite tra lo stupore e il timore, che sottende un riflesso spontaneo, un rifiuto oppure un disinteresse di fondo. Penso che ciò sia in parte causato dal fatto che la matematica non possa prescindere da una sua difficoltà intrinseca, perlopiù legata al linguaggio rigoroso e tecnico che la contraddistingue. Perciò qui, consapevole di come non possa scrivere in modo troppo tecnico, proverò a presentare della quasi matematica, una versione divulgativa che possa essere condivisa con un pubblico più ampio, ma che trattenga almeno parte della bellezza che si nasconde dietro quel muro impenetrabile ai più. Infatti, secondo me, la matematica è piena di arte ed eleganza, che risiedono nei dettagli e negli incastri perfetti, nella semplicità per descrivere fenomeni complessi.
Ecco dunque della quasi matematica, inspirata qui dalla controintuitiva nozione di quasi ovunque. Per arrivare a definire questo concetto, dovremo fare un breve excursus attraverso numeri naturali, numeri razionali, numeri reali, concetto di limite, e insieme di Cantor. Cominciamo.

Numeri naturali
I numeri naturali sono, come dice il nome, quelli con cui siamo naturalmente in contatto tutti i giorni. Zero, uno, due, tre, quattro, e così via. Notiamo che, dato ogni numero, per quanto grande sia, possiamo sempre aggiungerci uno in più. Dunque i numeri naturali sono infiniti. Ma già qui sorgono i primi problemi di formalizzazione matematica: cosa vuol dire infinito? Non preoccupiamocene troppo, almeno per il momento. D’altra parte, mentre l’umanità stava utilizzando questi numeri da millenni, la definizione rigorosa dei numeri naturali ha meno di 200 anni.

Numeri razionali
Passo successivo. Immaginiamo di avere un metro (per misurare) infinitamente lungo. Iniziamo scrivendo sul metro i numeri naturali: zero, uno, due, tre, eccetera. Successivamente, possiamo iniziare a segnare le frazioni, 1/2 (un mezzo), 4/3 (quattro terzi), 1/6 (un sesto) (fig. 1). Ci accorgeremo che già tra 0 e 1 possiamo scrivere infiniti numeri in forma di frazione. Questi vengono chiamati numeri razionali. Bene. Siamo soddisfatti? Purtroppo pare di no.

Numeri reali
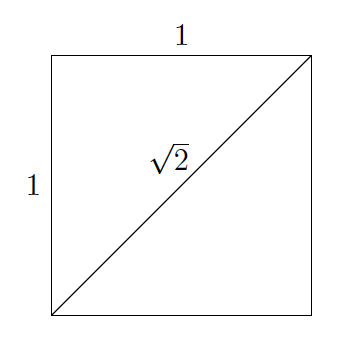
Per quante frazioni scriviamo, rimarranno sempre dei buchi, dei numeri sul metro non segnati. Infatti, già i matematici indiani intorno al 700 a.C. e i filosofi greci intorno al 400 a.C. si erano accorti che la radice di 2 (che è uguale alla lunghezza della diagonale di un quadrato di lato 1; fig. 2), non si può rappresentare come frazione. La soluzione è stata introdurre i numeri reali, cioè tutti i numeri sul metro, non solo quelli che si possono scrivere come numeri naturali o razionali (frazioni). Un esempio è per l’appunto la radice di 2, √2 in formule, che è un numero reale, ma non si può scrivere come frazione. Di nuovo, avere una definizione rigorosa ha richiesto molto tempo ed è arrivata anch’essa nella seconda metà del XIX secolo. Notare che nella nostra quotidianità percepiamo il continuo, e con questo intendo dire, per esempio, che percepiamo il metro come liscio, completo, e non con dei numeri mancanti. I numeri reali sono perciò molto utili per descrivere con modelli matematici la realtà intorno a noi.

Successioni e limiti
Dati i numeri reali, possiamo ora parlare del concetto di limite, che presentiamo con un esempio. Immaginiamo di avere una torta, mangiarne metà, poi mangiarne metà della rimanenza. E così via, continuando ad ogni passo a mangiare la metà della restante torta. In formule, supponiamo che la torta inizialmente pesi 1 (etto, ma in realtà non è importante specificare l’unità di misura). Dopo il primo assaggio, ne rimarrà 1/2, poi 1/4, poi 1/8, e così via (fig. 3). Quanta torta rimane alla fine? La risposta è il limite della successione di numeri

1, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, ...

Questo limite fa 0. In altre parole, alla fine non resta più nemmeno un briciolo di torta. Notare però che il numero di assaggini che dobbiamo fare per finire la torta è infinito. Supponiamo ora che ogni etto di torta richieda un minuto per essere mangiato. Quanto tempo ci si impiega a mangiare tutta la torta? Visto che il numero di assaggini che facciamo sono infiniti, ci si aspetterebbe che il tempo sia infinito. In realtà non è così. Al primo assaggio, mangiamo metà torta (mezzo etto), e quindi ci mettiamo mezzo minuto. Al secondo assaggio mangiamo un quarto di torta e quindi un quarto di minuto, e così via. In formule, il tempo totale per mangiare la torta sarà dato dalla seguente somma infinita

1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + …

La matematica è riuscita a dare un senso rigoroso a questa somma infinita, ottenendo che il risultato è 1. Dunque il tempo totale per mangiare tutta la torta è di solo 1 minuto. Per formalizzare questa somma infinita viene di nuovo utilizzato il concetto di limite. Infatti, diciamo che il risultato della somma infinita è il limite delle somme parziali, cioè il limite della successione

1/2,

1/2 + 1/4 = 3/4,

1/2 + 1/4 + 1/8 = 7/8,

1/2 + 1/4 + 1/8 + 1/16 = 15/16, …

Insieme di Cantor
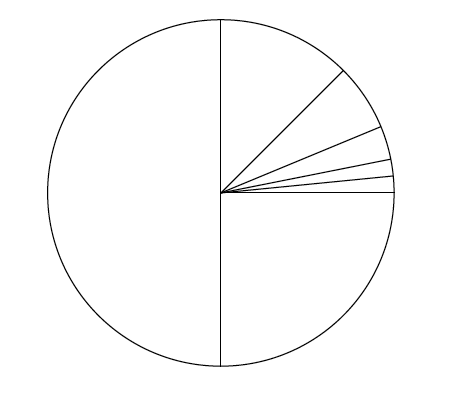
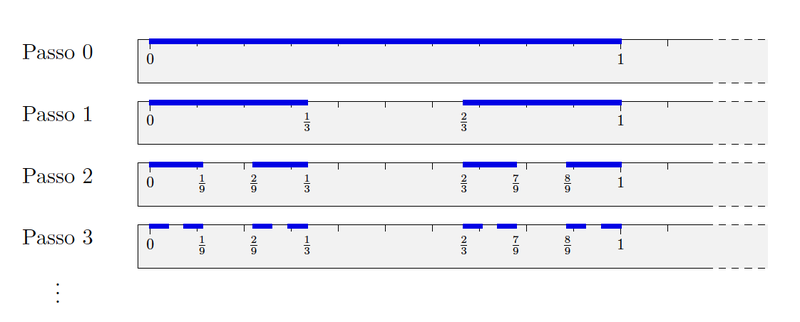
Immaginiamo ora quest’altro processo. Riprendiamo il metro di cui abbiamo parlato prima. Con una matita, disegniamoci sopra un tratto che collega i numeri 0 e 1. Al primo passo, cancelliamo il tratto di matita da 1/3 a 2/3. Ci ritroviamo dunque con due tratti (uno da 0 a 1/3 e uno da 2/3 a 1), entrambi di lunghezza 1/3. Al secondo passo, per ognuno di questi tratti, cancelliamo il terzo in mezzo. Continuiamo questo processo indefinitivamente. Ad ogni passo, sul metro ci saranno vari tratti di matita e, per ogni tratto, andremo a cancellare il terzo centrale del tratto. Rimandiamo alla figura in alto (dove i tratti in matita sono in bianco) per capire meglio il procedimento.
Come per la torta, supponiamo di poter fare questi infiniti passi in tempo finito. Cantor, intorno al 1880, dimostrò che in questo modo non cancelleremo tutto il segno di matita, anzi, quello che rimane è un insieme infinito, che oggi chiamiamo insieme di Cantor. Voglio accennare che Cantor si accorse anche che esistono varie ‘misure di infinito’ e l’insieme di Cantor risulta essere più grande dell’insieme dei numeri naturali, diciamo dunque che è innumerabile. Sembra filosofia, in parte probabilmente lo è, e inizialmente questo risultato è stato accolto con molto scetticismo dalla comunità matematica.
Vogliamo ora cercare di capire qual è la lunghezza totale dell’insieme di Cantor, o in altre parole della matita che è rimasta sul foglio dopo le nostre operazioni. Siamo partiti con un tratto di lunghezza 1. Abbiamo cancellato un tratto di lunghezza 1/3, dunque la lunghezza dei due tratti restanti è 2/3. Per ognuno di questi tratti ne abbiamo cancellato un terzo, perciò la lunghezza dei quattro tratti restanti è 2/3 - 1/9 - 1/9 = 4/9. E così via, ai passi successivi otterremo 8/27, 16/81, etc. La lunghezza dell’insieme di Cantor è data dal limite di questa successione infinita di numeri, che risulta essere 0! Dunque, l’insieme di Cantor è grandissimo, innumerabile, ma la sua lunghezza totale è 0. Come è possibile? La risposta risiede nella struttura molto particolare di questo insieme e nel fatto che il concetto di lunghezza per un tale insieme non è intuitivo.
In generale, diciamo che un insieme (cioè un gruppo) di numeri reali ha misura nulla se ha ‘lunghezza totale’ uguale a zero. Alternativamente, diciamo che quasi tutti i numeri reali non appartengono all’insieme. Nel caso dell’insieme di Cantor e della nostra costruzione, possiamo dire che il metro non ha segni di matita quasi ovunque. Il concetto di quasi ovunque ha molte applicazioni in matematica. Un esempio semplice e diretto riguarda la teoria della probabilità. Immaginiamo di dover misurare un tavolo con il nostro metro infinitamente preciso. La probabilità che il numero che otteniamo appartenga all’insieme di Cantor è nulla, questo perché quasi tutti i numeri sul metro non sono segnati in matita. Probabilità nulla, in matematica, significa che l’evento è talmente raro che non succede praticamente mai.
Quasi mai. Proprio in questa parola si gioca il rapporto tra noi e l’uso che facciamo del concetto di limite che per definizione include entro di sé il quasi, un tendere che dovrebbe non arrivare mai, eppure... e dacché iniziamo a giocare con l’infinito, a sua volta incluso nel concetto di limite e quindi strettamente legato al quasi, le cose più assurde diventano reali: che c’è di strano se l’insieme di Cantor è quasi nullo, ma allo stesso tempo innumerabile?